Capítulo 3: Operaciones con números binarios en el microprocesador
3.1 Introducción
En una computadora, las operaciones aritméticas se realizan en 8 bits, 16 bits, 32 bits o 64 bits. Un número como 3 en binario es 11. Si la operación se va a realizar en 8 bits, este se considera como 00000011; precedido por 0 ceros.
Para un número binario como 10000101, el bit más significativo es el bit del extremo izquierdo. Es 1 en este caso. El bit menos significativo es el bit extremo a la derecha, que sigue siendo 1, para el número. El bit más significativo se abrevia como MSB. El bit menos significativo se abrevia como LSB.
El dígito BInario se abrevia como BIT y se escribe simplemente como bit. En el número 10010011, cada uno o cero es un bit. Un grupo de cuatro bits se llama mordisco. Un grupo de ocho bits se llama byte. Un byte consta de dos nibbles. El cuarteto inferior es el cuarteto del LSB y el cuarteto más alto es el cuarteto del MSB.
Un grupo de 8 bits, 16 bits, 32 bits o 64 bits se denomina palabra, siempre que ese grupo transmita información más allá de simplemente indicar un número. El grupo se denomina palabra, por ejemplo, si se trata de una instrucción de bajo nivel en la computadora. También existe una palabra de 24 bits, pero que hoy en día no se utiliza habitualmente.
La endianidad se refiere al orden en el que los bytes forman una palabra. Considere la palabra de 24 bits: 100100001111010100100010. Esta palabra consta de tres bytes que son:
10010000 11110101 00100010
El byte más significativo es el byte más a la izquierda. Cuando el byte del extremo izquierdo es el byte más significativo y el byte del extremo derecho es el byte menos significativo, esto se denomina representación Big Endian de la palabra. La representación de Little Endian es todo lo contrario.
La memoria de la computadora es una serie de celdas y cada celda contiene un byte. La primera celda de la memoria de la computadora es para el byte 0, la segunda es para el byte 1, la tercera es para el byte 2, y así sucesivamente. Con big endianness y para la palabra anterior, el byte más significativo se almacena en la celda del byte 0, el byte del medio se almacena en la celda del byte 1 y el byte menos significativo se almacena en la celda del byte 2. Esto significa que hay bytes más significativos en la celda de memoria inferior.
La palabra anterior de 24 bits se puede escribir en orden inverso de bytes de la siguiente manera:
00100010 11110101 10010000
Ahora, el byte menos significativo está en el extremo izquierdo y el byte más significativo está en el extremo derecho. Cuando el byte del extremo izquierdo es el byte menos significativo y el byte del extremo derecho es el byte más significativo, es la representación Little Endian de la palabra. Con poca endianidad y para la palabra anterior, el byte menos significativo se almacena en la celda del byte 0, el byte del medio se almacena en la celda del byte 1 y el byte más significativo se almacena en la celda del byte 2. Esto significa que hay un byte menos significativo en la celda de memoria inferior.
La endianidad no se utiliza para los bits de un byte. Tampoco se utiliza para nibbles en un byte. Sólo se utiliza para el orden de bytes.
La recta numérica
Un número sin signo es un número positivo. Los números positivos son números que van desde cero hacia arriba. También existen números negativos. Los números positivos y negativos se pueden presentar en una recta numérica. La siguiente recta numérica muestra los números enteros positivos y negativos (enteros) cerca de cero:
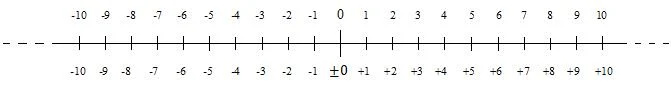
Los números negativos disminuyen de cero hacia abajo (hacia la izquierda). En muchas situaciones, el cero se considera positivo. Sin embargo, en algunas situaciones se considera negativo. Por eso hay un signo más y menos delante del cero, en la numeración inferior, en el diagrama. Cuando un número es positivo, se puede omitir su signo; este es el caso de la numeración superior del diagrama. El signo menos delante de un número negativo nunca se omite.
3.2 Suma de números binarios
Además:
A + B = S
A se llama sumando, B se llama sumando y S se llama suma.
Considere la siguiente suma de dos números positivos en base dos:

En base dos, los únicos dígitos posibles son 0 y 1. La suma en base 2 es similar a la suma en base diez, pero dos en base dos es uno-cero (10). Cuando la suma de dos bits en una columna es 10, se escribe 0 y se lleva 1 a la columna inmediata de la izquierda; que se sumará a la suma de los dos bits allí. Cuando la suma total es tres, significa 11 en base dos. Se escribe el 1 derecho en 11 y el 1 izquierdo se lleva para agregarlo a la suma de los bits inmediatos de la columna izquierda. En cualquier caso, el 1 llevado hacia la izquierda se llama acarreo.
Leyendo la tabla de suma anterior desde la derecha, en la segunda columna (desde la derecha), hay un acarreo que resulta de 1+1 = 10. En la tercera columna, hay un acarreo que resulta de 1+1+ acarreo de 1 = 11. En la cuarta columna, hay un acarreo que resulta de 0+1+ acarreo de 1 = 10. En la quinta columna, no hay acarreo porque la sumatoria es 0+0+ acarreo de 1 = 1. El El resto de las columnas no implica acarreo.
El recuento de columnas comienza desde el extremo derecho. Con la suma de 16 bits, puede haber un acarreo de la octava columna a la novena columna (moviéndose hacia la izquierda). La siguiente tabla ilustra esto:

Las operaciones aritméticas y lógicas se realizan en el microprocesador de la placa base del ordenador.
Para una computadora de 8 bits, el acarreo no puede pasar del octavo al noveno bit automáticamente por hardware. Entonces, para agregar dos grupos de 16 bits en una computadora de este tipo, la suma debe realizarse dos veces en pares de ocho u ocho bits. El transporte se mueve y se realiza mediante software (programación).
Para sumar dos números, los números se pueden convertir primero a su forma de complemento a dos (ver más abajo) antes de sumar.
3.3 Complemento a dos y su resta de números binarios
En la placa base de la computadora está la memoria y el microprocesador y otros circuitos. La memoria es una serie de celdas de ocho bits. En un byte, cada bit va a una celda. El microprocesador tiene algunas ubicaciones de tipo memoria. Estas ubicaciones de tipo memoria se denominan registros. Así, en una computadora, se pueden almacenar temporalmente grupos de bytes en la memoria o en los registros del microprocesador.
En cualquiera de estos almacenes, cada celda puede contener un 1 o un 0, y nada más. En la vida hay números positivos y negativos. Un número positivo comienza con un signo más (+) y un número negativo comienza con un signo negativo (-). Cuando se omite el signo, el número se considera positivo.
Para solucionar este problema de indicar el signo de un número en la computadora, los números enteros se almacenan en rangos. Los números enteros son números enteros. Si se utilizan ocho bits para almacenar el rango de números posibles, el bit más a la izquierda se utiliza como bit de signo. Si el número comienza con 0, el número es un número positivo. Si comienza con 1, el número es un número negativo. Si se utilizan dieciséis bits para almacenar el rango de números posibles, el bit más a la izquierda se utiliza como bit de signo. Si el número comienza con 0, el número es un número positivo. Si comienza con 1, el número es un número negativo. Los números en este formulario se llaman números con signo.
En la práctica, puede haber números con signo para 8 bits, 16 bits, 32 bits y 64 bits. Cuanto mayor sea el número de bits utilizados, mayor será el rango de números posibles que se pueden almacenar.
Enteros en complemento a dos
Con el complemento a dos, los números positivos son los números de conteo normales, excepto que el dígito más a la izquierda es 0. Para obtener el número negativo correspondiente a cualquier número positivo dado, invierte cada bit del número y suma 1 al resultado. El inverso o complemento de 0 es 1. El inverso o complemento de 1 es 0. Las siguientes tablas muestran algunos números en complemento a dos en sus rangos:
| Tabla 3.31 Enteros en complemento a dos en dos bits |
|
|---|---|
| Binario | Decimal |
| 01 | +1 |
| 00 | +0 |
| 11 | -1 |
| 10 | -2 |
Los números binarios positivos son 00 y 01 (es decir, cero y uno). En el bit más a la izquierda, el cero muestra que son números positivos. 00 está algo en el medio del rango. Para obtener -1, se encuentra que el inverso del número 01 es 10. Sumar 1 a esto (en el extremo derecho) da 11.
Dado que se utilizan dos bits, solo queda un bit para representar los números en el rango que consta de los números +1, +0 y -1 correspondientes a 01, 00 y 11. El primer bit indica el signo. Sucede que 10 por +2 no se encuentra entre estos tres números binarios. 10 comienza con 1, lo que significa que debe ser un número negativo en complemento a dos. Entonces, 10 está incluido en el rango, lo que significa -2.
Con dos bits en complemento a dos, el número de todos los números enteros (positivos y negativos) que se pueden representar es 2 2 = 4 y no 2 2 -1 = 3. El matiz resulta de la inclusión del último número negativo que es el negativo de 2 numerocon – 1. En este caso, -2 2-1 = -2 1 = -2. No hay +2 en el rango de números en complemento a dos en 2 bits.
| Tabla 3.32 Enteros en complemento a dos en cuatro bits |
|
|---|---|
| Binario | Decimal |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
Los números binarios positivos van del 0000 al 0111 (es decir, del cero al siete). En el bit más a la izquierda, el cero muestra que son números positivos. 0000 está algo en el medio del rango. Para obtener -1, el inverso del número 0001 resulta ser 1110. Sumar 1 a esto (en el extremo derecho) da 1111. Para obtener -2, el inverso de 0010 resulta ser 1101. Sumar 1 a esto ( desde el extremo derecho) da 1110. Los otros números binarios negativos como -3 a -7 se determinan de manera similar.
Como se utilizan cuatro bits, quedan tres bits para representar los números en el rango que son +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 y -7 correspondientes a 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 y 1001.
El -8 que corresponde a 1000 debe abordarse por separado. El primer bit de todos estos números indica el signo de 0 para números positivos y 1 para números negativos. Sucede que 1000 no se encuentra entre estos catorce números binarios. 1000 comienza con 1, lo que significa que tiene que ser un número negativo, en lo que respecta al complemento a dos. Entonces, 1000 está incluido en el rango, lo que significa -8.
Con cuatro bits en complemento a dos, el número de todos los números enteros (positivos y negativos) que se pueden representar es 2 4 = 16 y no 2 4 – 1 = 15. El matiz resulta de la inclusión del último número negativo que es el negativo de 2 númeroAncho – 1. En este caso, -2 4 -1 = -2 3 = -8. No hay +8 en el rango de números.
El análisis anterior para dos, cuatro y más bits en complemento a dos se puede aplicar a números binarios de 8 bits, 16 bits, 32 bits y 64 bits de ancho.
El complemento a dos sacrifica el primer bit (el más a la izquierda) por el signo de 0 para un número positivo y 1 para un número negativo. Para el grupo de bits de “n” bits de ancho, hay 2 norte total de números positivos más negativos. Serían 2 norte -1, si no fuera por el último número negativo (el más pequeño) de la suerte incluido. El número positivo más alto es +2. n-1 -1 y el número negativo más pequeño es -2 n-1 -1. Seria -2 n-1 -1, si no fuera por los afortunados -2 n-1 incluido.
Restar números en complemento a dos
En resta:
A – B = D
A se llama minuendo, B se llama sustraendo y D se llama diferencia.
Para restar un número binario positivo de otro número binario positivo, el minuendo se escribe en complemento a dos y el sustraendo se convierte a su valor negativo en complemento a dos. Entonces, el enunciado matemático queda:
A+ – B = D
En otras palabras, en la resta en complemento a dos, el sustraendo se convierte en un número negativo y luego se suma al minuendo.
Ejemplo 3.31:
Evalúe la siguiente expresión decimal en complemento a dos usando cuatro bits:
6 – 4
Solución:
El número binario para 6 es 110. En complemento a dos de 4 bits, es 0110. El número binario para +4 es 100. En complemento a dos de 4 bits, es 0100. 0100 que debe convertirse a 4 negativo en dos complemento de la siguiente manera: El complemento o inversión de 0100 es 1011. Sumarle 1 a esto desde el extremo derecho, como hicimos además, da 1100. Entonces, la expresión decimal es:
6 – 4 que se convierte en:
0110 – 0100 que es
0110 +(– 0100) = 0110 + 1100 hecho como en la sección de suma anterior como:

Nota: 0110 +(– 0100) es lo mismo que 6 + – 4
Con la resta en complemento a dos, cualquier acarreo, después de la última columna hacia la izquierda, en la suma, se descarta. Al restar en decimal, el enunciado matemático es:
6 – 4 = 2
Haciendo lo mismo en complemento a dos, la respuesta es 0010, que es +2 en el conteo binario en complemento a dos. La resta anterior resta un número menor de un número mayor. En el siguiente ejemplo, un número mayor se resta de un número menor. Se puede consultar la tabla 3.32 para ver si 0010 es realmente complemento a dos, lo que equivale a +2.
Ejemplo 3.32:
Evalúa la siguiente expresión decimal en complemento a dos con cuatro bits:
4 – 6
Solución:
El número binario para 4 es 100. En complemento a dos de 4 bits, es 0100. El número binario para +6 es 110. En complemento a dos de 4 bits, es 0110. 0110 debe convertirse a 6 negativo en complemento a dos de la siguiente manera: El complemento o inversión de 0110 es 1001. Sumarle 1 desde el extremo derecho, como hicimos en la suma anterior, da 1010. Entonces, la expresión decimal es:
4 – 6 que se convierte en:
0100 – 0110 que es
0100 +(– 0110) = 0100 + 1010 hecho como en la sección de suma anterior como:

Nota: 4+ – 6 es lo mismo que 0100 +(– 0110).
Con la resta en complemento a dos, cualquier acarreo, después de la última columna hacia la izquierda, en la suma, se descarta. Al restar en decimal, el enunciado matemático es:
4 – 6 = -2
Haciendo lo mismo en complemento a dos, la respuesta es 1110, que es -2 en el conteo binario en complemento a dos. Se puede consultar la tabla 3.32 para ver si 1110 es realmente complemento a dos, lo que equivale a -2.
3.4 Multiplicación de números binarios
En el comunicado:
A x B = P
A se llama multiplicando, B se llama multiplicador y P se llama producto. La expresión A x B significa sumar A, B varias veces cuando A y B son números enteros (números enteros).
La multiplicación en binario es lo mismo que la multiplicación en decimal. Sin embargo, en lugar de hacerlo en decimal, se hace en binario. La multiplicación de la expresión decimal de 42 x 10 se realiza en binario de la siguiente manera donde 42 10 = 101010 2 y 10 10 = 1010 2 :
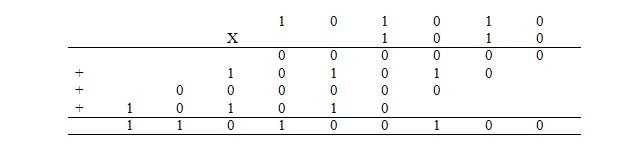
Los 4 números que se suman se denominan productos parciales. La respuesta es el producto. La suma de los productos parciales se realiza de la misma forma explicada anteriormente.
La multiplicación también se puede ver de la siguiente manera: en esta multiplicación en base dos, si el bit (dígito) en el multiplicador es 1, el bit menos significativo de su producto parcial es el bit menos significativo del multiplicando que se vuelve a escribir directamente debajo de él; y el resto de bits del multiplicando se repiten hacia la izquierda. En esta multiplicación de base dos, si el bit (dígito) en el multiplicador es 0, su producto parcial consta de 0 con el bit menos significativo de 0 directamente debajo de él. El número de todos los ceros es el número de bits del multiplicando.
3.5 División de números binarios
En el comunicado:
A ÷ B = Q
A se llama dividendo, B se llama divisor y P se llama cociente. El cociente puede ir acompañado de un resto. La expresión A ÷ B significa cuántas veces se puede sumar B para obtener A o estar cerca de él de modo que el resto sea 0 o menor que B.
La división se puede hacer de muchas maneras. La división que se muestra aquí es la división de restauración.
División restauradora
Este es el método de división larga que se aprende en las escuelas. Si 237 se divide entre 6, la respuesta es 39 resto 3. El 237 10 en base 2 es 11101101 2 y 6 10 en base 2 es 110 2 . el 39 10 en base 2 es 100111 2 y 3 10 en base 2 es 11 2 .
Entonces, 11101101 2 dividido por 110 2 da 100111 2 resto 11 2 en base dos. Con el método de restauración, los números binarios son números ordinarios y no necesariamente están en complemento a dos. La siguiente estructura divide 11101101 2 por 110 2 dar 100111 2 resto 11 2 :

La resta se hace normalmente y no usando el complemento a dos. Como se trata de base dos, un préstamo es dos y no diez. Los dividendos parciales son 10, 101, 1011, 1010 y 1001. 11 es el resto. Como el divisor tiene tres dígitos, la división se realiza básicamente en grupos de tres dígitos del dividendo dado. El cociente es el número entero (entero) y es 100111 para este problema. El resultado del cociente y el resto es el esperado.
3.6 Operaciones aritméticas con software y hardware
La placa base de la computadora tiene un reloj. Los tictac del reloj se llaman pulsos. En cada pulso de reloj, se toman una o más decisiones en diferentes lugares de la placa base; y eso tiene que ver con la programación (software).
Dentro del microprocesador existen dos tipos de circuitos llamados: Circuitos Lógicos Combinacionales y Circuitos Lógicos Secuenciales. Existe otro tipo de circuito llamado multiplexor. La suma, multiplicación y división se pueden realizar dentro de un intervalo de reloj utilizando la lógica combinacional (circuito). Mientras que la programación (software) confirma la decisión en cada pulso de reloj utilizando circuitos lógicos secuenciales y multiplexores.
Cuando la resta se realiza utilizando el complemento a dos, se necesitan al menos dos pulsos de reloj. En el primer pulso de reloj, un multiplexor canaliza el sustraendo a un conjunto de puertas NOT (una puerta NOT por dígito). En el segundo pulso de reloj, la lógica combinacional suma 1 a la salida de las puertas NOT y continúa sumando el sustraendo y minuendo resultantes. Toda esa adición puede tener lugar dentro de un intervalo de reloj.
La suma, la multiplicación y la división aún pueden funcionar con la programación utilizando tablas de verdad. Sin embargo, no está cubierto en este curso profesional en línea.
3.7 Operaciones Lógicas en el Microprocesador
Y, O, XOR e Invertir
Y
La siguiente tabla ilustra el AND bit a bit. Esto significa que para dos números binarios diferentes, los bits correspondientes reciben una operación AND según la tabla de verdad AND:
Moviéndose de izquierda a derecha, 1 Y 1 = 1; 0 Y 1 = 0; 0 Y 0 = 0; 1 Y 0 = 0; y así sucesivamente de acuerdo con la tabla de verdad AND.
O
La siguiente tabla ilustra el OR bit a bit. Esto significa que para dos números binarios diferentes, los bits correspondientes se someten a una operación OR según la tabla de verdad OR:

Moviéndose de izquierda a derecha, 1 O 1 = 1; 0 O 1 = 1; 0 O 0 = 0; 1 O 0 = 1; y así sucesivamente de acuerdo con la tabla de verdad OR.
GRATIS
La siguiente tabla ilustra el OR exclusivo bit a bit. Esto significa que para dos números binarios diferentes, los bits correspondientes se someten a XOR según la tabla de verdad XOR:

Moviéndose de izquierda a derecha, 1 XOR 1 = 0; 0 XOR 1 = 1; 0 XOR 0 = 0; 1XOR 0 = 1; y así sucesivamente de acuerdo con la tabla de verdad XOR.
Invertir (NO)
La siguiente tabla ilustra el NOT bit a bit (invertido). Esto significa que para un número binario, esta vez, cada bit se invierte según la tabla de verdad NOT:

Moviéndose de izquierda a derecha, NO 1 = 0; NO 0 = 1; NO 0 = 1; NO 1 = 0; y así sucesivamente de acuerdo con la Tabla de Verdad NOT.
Desplazarse hacia la derecha o hacia la izquierda
Desplazamiento a la derecha
El siguiente número binario se desplaza 3 posiciones de bits hacia la derecha, con los ceros insertados en las posiciones de bits desocupadas a la izquierda:

El cambio se puede realizar para una, dos, tres, cuatro, etc. plazas.
Desplazamiento a la izquierda
El siguiente número binario se desplaza 3 posiciones de bits hacia la izquierda, con los ceros insertados en las posiciones de bits desocupadas a la derecha:

El cambio se puede realizar para una, dos, tres, cuatro, etc. plazas.
Girar hacia la derecha o hacia la izquierda
Girar es similar a cambiar. Se hace poco a poco. Al girar hacia la derecha, las puntas que salen del extremo derecho no se caen como en el desplazamiento; reemplazan los bits desocupados a la izquierda, uno por uno. Al girar hacia la izquierda, las puntas que salen del extremo izquierdo no se caen como en el desplazamiento; reemplazan los bits desocupados a la derecha, uno por uno.
Gira a la derecha
El siguiente número binario se gira 3 posiciones de bits hacia la derecha:

La rotación se puede realizar en uno, dos, tres, cuatro, etc. lugares.
Rotar a la izquierda
El siguiente número binario se gira 3 posiciones de bits hacia la izquierda:

La rotación se puede realizar en uno, dos, tres, cuatro, etc. lugares.
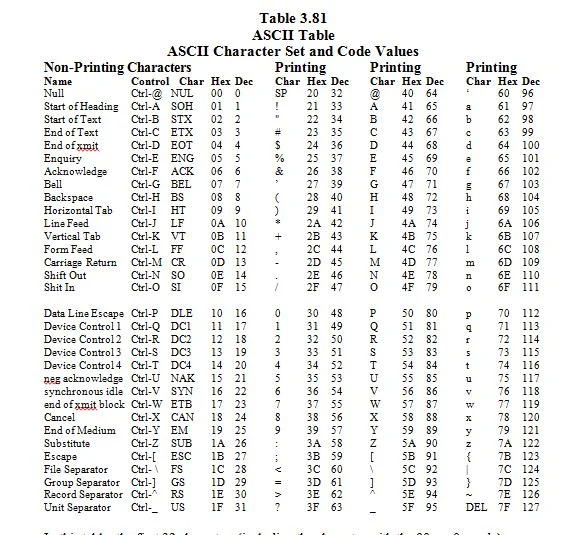
3.8 Juego de caracteres ASCII y sus valores de código
ASCII significa “Código estándar estadounidense (EE. UU.) para el intercambio de información”. Imagina un teclado con 96 teclas. Este es un teclado ideal donde las teclas de letras mayúsculas son diferentes de las teclas de letras minúsculas. Cada dos teclas representan un carácter que se encuentra en un teclado en inglés (EE. UU.). Los caracteres y códigos (números correspondientes a los caracteres) se enumeran a continuación:
En esta tabla, los primeros 32 caracteres (incluido el carácter con el 00 16 = 0 10 código) son caracteres que no se imprimen. Son personajes de control. No se ven en la pantalla (monitor) donde están todos iguales. Sólo tienen efectos. Discutamos más sobre eso más adelante.
El resto de personajes son caracteres impresos; se ven en la pantalla. Hay 128 caracteres ASCII. 2 7 = 128. 1,111,111 2 = 127 10 . El 7 en 2 7 significa 7 bits.
Ahora, 1111111 2 + 1 2 es lo mismo que:
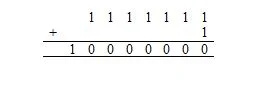
Aquí, 10.000.000 2 = 128 10 . Hay 128 10 caracteres de la lista (tabla) anterior de caracteres ASCII. Esto incluye el carácter nulo, cuyo código en base dieciséis (hexadecimal) es 00, que equivale a 0 en base diez.
Dado que hay 128 caracteres en total, 128 menos 32 caracteres no imprimibles dan 96 caracteres imprimibles. En esta sección se supone que hay un teclado ideal con 96 caracteres que son caracteres imprimibles. En este teclado ideal, las teclas de los caracteres ingleses en mayúsculas son diferentes de las teclas de los caracteres ingleses en minúsculas.
Cada carácter del teclado está representado por un número de base dos de 7 bits que no se muestran en la lista. La letra mayúscula de “N”, por ejemplo, está representada por los siete bits 1001110 en base 2. Para convertir 1001110 2 en base 16, precedido por 0 y agrupar el resultado en subgrupos de cuatro bits de la siguiente manera:
| 0100 | 1110 | 2 = | 4 | mi | 16
Ese es 01001110 2 = 4E 16 . Para convertir 4E 16 a base diez, haga lo siguiente:
4x (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
A la derecha de 'N' en la lista (tabla) está el número hexadecimal de 4E y el número decimal de 78.
Como otro ejemplo, el carácter “[“ está representado por los siete bits 1011011 en base 2. Para convertir 1011011 2 en base 16, precedido por 0 y agrupar el resultado en subgrupos de cuatro bits de la siguiente manera:
| 0101 | 1011 | 2 = | 5 | B | 16
Ese es 01011011 2 = 5B 16 . Para convertir 5B16 a base diez, haga lo siguiente:
5x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
A la derecha de '[' en la lista (tabla) está el número hexadecimal de 5B y el número decimal de 91.
Como otro ejemplo más, el carácter del número decimal “5” está representado por los siete bits 0110101 en base 2, y no 0000101 en base 2. Para convertir 0110101 2 en base 16, precedido por 0 y agrupar el resultado en subgrupos de cuatro bits de la siguiente manera:
| 0011 | 0101 | 2 = | 5 | B | 16
Ese es 00110101 2 = 35 16 . Para convertir 3516 a base diez, haga lo siguiente:
3x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
A la derecha de “5” en la lista (tabla) está el número hexadecimal de 35 y el número decimal de 53.
Dado que la computadora funciona en bytes, cuando se presiona una tecla en el teclado ideal, se envían ocho bits al microprocesador (placa base). El teclado ideal es un periférico que está separado de la unidad del sistema (base) de la computadora. Tiene un circuito electrónico (IC) que crea los siete bits y los precede con un cero antes de enviarlos a través de su cable a la placa base de la unidad del sistema. Desde el puerto de entrada (circuito de entrada) de la placa base, va al microprocesador que también está en la placa base. Del microprocesador pasa a la memoria que también está instalada en la placa base.
Entonces, cuando se presiona la tecla “N” en el teclado ideal, se llevan ocho bits 01001110 al microprocesador. Desde el microprocesador son llevados a la memoria donde permanecen en una ubicación de memoria como un byte. El programador informático debe tener en cuenta que los ocho bits de 01001110 2 es lo mismo que 4E 16 que es lo mismo que 78 10 .
Cuando se presiona la tecla “[“en el teclado ideal, se llevan ocho bits 01011011 al microprocesador. Desde el microprocesador son llevados a la memoria donde permanecen en una ubicación de memoria como un byte. El programador informático debe tener en cuenta que los ocho bits de 01011011 2 es lo mismo que 5B 16 que es lo mismo que 91 10 .
Cuando se presiona la tecla “5” en el teclado ideal, como carácter y no como número decimal, se llevan ocho bits 00110101 al microprocesador. Desde el microprocesador son llevados a la memoria donde permanecen en una ubicación de memoria como un byte. El programador informático debe tener en cuenta que los ocho bits de 00110101 2 es lo mismo que 35 16 que es lo mismo que 5310 10 .
Hay ocasiones en las que un programa se está ejecutando y espera a que se ingrese el número decimal 5 en la computadora. En esta situación, si se presiona la tecla '5' en el teclado ideal, aún así se lleva el código de ocho bits 00110101 al microprocesador. Como lo que se necesita es el número decimal 5, y no el carácter “5”, un fragmento de código (programa corto) de la memoria utiliza el microprocesador para convertir el código de carácter 00110101 en base dos al número en complemento a dos 00000101. 2 antes de enviarlo a una ubicación de memoria como un byte en complemento a dos. El programador informático debe tener en cuenta que 00000101 significa 5 10 en base 2, y es diferente a los números de código de 00110101 2 , 35 16 y 53 10 que significa el carácter de “5”. Para mostrar el número en complemento a dos de 00000101 en la memoria, otro programa corto tiene que convertir 00000101 de la memoria a 00110101. Es 00110101, que es lo mismo que 35. 16 que es lo mismo que 53 10 que se muestra en el monitor (o se imprime en un papel con la impresora).
3.9 Formato de número de punto flotante
Un número sin parte decimal es un número entero. El número 36 es un número entero. 36,375 no es un número entero. Es un número decimal con una parte decimal. La parte decimal de .375 es una fracción menor que 1.
36.375 se interpreta en forma decimal como:
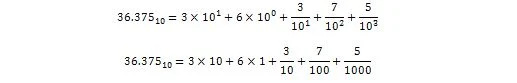
Ahora:
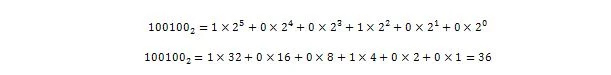
Entonces, 100100 2 = 3610 que es la parte entera de 36.375 10 .
Ahora:
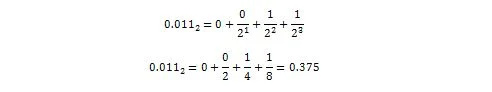
Entonces, 0.011 2 = 0.375 10 cual es la parte decimal de 36.375 10 .
∴ 36.375 10 = 100100.011 2
Dicho de otra manera:
100100.011 2 = 36.375 10
Los números se representan en el ordenador en base 2 y no en base 10, siendo todo igual. Dado que una celda en un registro del microprocesador o una celda en la memoria sólo puede tomar 1 o 0, no hay espacio para almacenar un punto decimal. Esto plantea un problema. Como resolución, existe la representación de coma flotante de 32 bits de precisión simple IEEE-754 y la representación de coma flotante de 64 bits de precisión doble IEEE-754.
Formato de número de coma flotante de 32 bits
El número 100100.0112 se puede expresar como:
100100.011 2 = 1.00100011 2 x2 +5
El lado derecho del símbolo = se conoce en matemáticas como la forma estándar de base dos del lado izquierdo de 100100.011. 2 .
Ahora, 00100011 de 1.00100011 2 en el lado derecho del símbolo =, sin el '1' anterior. y sin el 2 para la base, se llama significado explícito. En este caso, el punto binario se lleva cinco lugares a la izquierda para tener el “1”. No confundas entre punto decimal y punto binario. El punto binario es para base 2, mientras que el punto decimal es para base 10. El '1'. seguido de 00100011 en el lado derecho del símbolo =, sin el 2 como base, forma el verdadero significado. Sin embargo, 1,00100011 se denomina significado implícito.
Después del significado en el lado derecho está el 'x 2 +5 ' expresión. Con esta expresión, el +5 se llama exponente. El signo más significa que el punto binario debe moverse cinco lugares hacia adelante para estar en su posición original normal y 2 es la base de la numeración. La ecuación anterior se puede escribir a la inversa como:
1.00100011 2 x2 +5 = 100100.011 2
Con la representación de coma flotante de 32 bits, es “1.00100011 2 x2 +5 ” que se utiliza y no solo “100100.011 2 ”. El 2 de la base no está registrado. La representación de coma flotante de 32 bits para “1.00100011 2 x2 +5 ”número, que es igual a 36.375 10 = 100100.011 2 , se muestra en la siguiente tabla:

Hay posiciones de 32 bits numeradas desde el extremo derecho, comenzando desde 0. El primer bit del extremo izquierdo es el bit de signo. Si el número es positivo, este bit es 0. Si el número es negativo, este bit es 1 (-1 consta de dos caracteres y no se puede colocar en ninguna celda). El 1.00100011 2 x2 +5 que es igual a 36.375 10 que también es igual a 100100.011 2 es un número positivo. Entonces el primer bit es 0.
Hay ocho posiciones de bits para el exponente, comenzando desde la posición 30 hasta la posición 23, inclusive. Sin embargo, el exponente que está escrito ahí es 10000100 2 que es igual a 132 10 . El exponente del número de interés es en realidad +5 en base dos. ¿Así que lo que ocurre?
Ahora, en el formato de 32 bits, un exponente de 0 se escribe como 01111111 2 que es igual a 127 10 . El +5 10 es +101 2 . Entonces, al llegar a 10000100 2 en la parte del exponente de la tabla, 101 2 fue agregado a 01111111 2 , correspondientemente. Significa que a 127 se le sumó 5 para tener 132. 10 .
El significado, sin “1.”, bajó las posiciones 22 a 15, inclusive. Tenga en cuenta que el 1 de '1.' no se ha indicado en la cadena de 32 bits. Nunca está indicado, acéptalo. El resto de las celdas hasta la posición 0 están llenas de ceros.
Si el exponente real es -5, entonces se resta 5 de 127 10 tener 122 10 . Esto corresponde a restar 101. 2 desde 01111111 2 tener 01111010 2 .
Con toda la ilustración anterior, el número +1 que es igual a 1.0 x 2 0 = 1,0 x 1 = 1,0 se representa como:

Tenga en cuenta que el '1.' de 1,0 x 2 0 no está indicado en el formato. Nunca está indicado. La siguiente fracción mixta que va positivamente después de 1,0 es:

Observe el 1 en el extremo derecho. Esta representación es el número:

La diferencia entre 1.0000001192092896 y 1.0 es:
1.0000001192092896 – 1.0 = 0.0000001192092896
Los números con parte decimal son fracciones mixtas. No todas las fracciones entre 1 10 y 2 10 se puede representar en el ordenador. Se puede suponer que la diferencia fraccionaria más pequeña entre números mixtos consecutivos con formato de coma flotante de 32 bits es 0,0000001192092896. Espere que el intervalo de doble precisión sea menor. Consulte la siguiente ilustración.
Al representar el número, 0,0 no sigue los argumentos anteriores. La representación de 0.0 está declarada y debe aprenderse como tal. Para representar 0,0, todas las celdas del significado son 0 y todas las celdas del exponente también son cero. El bit de signo puede ser 0 o 1. Desafortunadamente, esto da lugar a 0 positivo y 0 negativo de la siguiente manera:

En la vida real sólo hay un cero. El 0 positivo y el 0 negativo no existen. Sin embargo, 0 normalmente se considera positivo. Aquí existen 0 positivos y 0 negativos debido a esta descripción de formato particular. La recta numérica (ver arriba) también puede tener +0 y -0, pero solo existe un cero.
Formato de número de coma flotante de 64 bits
El formato de coma flotante de 64 bits es similar al formato de 32 bits, pero con las siguientes diferencias:
- Hay 64 bits para representar un número.
- Después del bit de signo, hay 11 bits para el número exponente.
- El número exponente para el índice cero (2 0 ) es 1023 10 = 01111111111 2 .
- Los once bits van seguidos de 52 bits para el significado explícito.
- Tiene una gama de números más amplia que el formato de 32 bits.
Tenga en cuenta que el '1.' que está al principio del significado todavía no está incluido entre los 64 bits, del mismo modo que no está incluido entre los 32 bits para el formato de 32 bits.
Una de las diferencias más importantes entre el formato de 64 bits y el de 32 bits es que la diferencia entre las fracciones mixtas consecutivas en el formato de 64 bits es menor que la del formato de 32 bits.
En el formato de 64 bits, el intervalo (espacio) entre 1,0 y la siguiente fracción mixta se puede calcular de la siguiente manera:
1.0 es
0 01111111111 00000000000000000000 00000000000 000000000000000000000 2
Esto equivale al “1.”, que no ha sido indicado en la cadena, multiplicado por 2 elevado a la potencia (índice) 0 (siendo el exponente 1023 10 = 01111111111 2 para 2 0 = 1). La cuerda es de 1,0 x 2 0 .
La siguiente fracción mixta mayor que 1,0 es:
0 01111111111 00000000000000000000 00000000000 000000000000000000001 2
Esto equivale a '1'. que no está indicado en la cadena, seguido de 51 ceros, y luego 1, multiplicado por 2 elevado a la potencia 0 (con el exponente 1023 10 = 011111111112 2 para 2 0 = 1). Esto es lo mismo que:
+2 0 × (1 + 2− -52 ) ≈ 1.0000000000000002
El ≈ significa aproximadamente igual a.
Ahora:
1.0000000000000002 – 1.0 ≈ 0.0000000000000002
El valor de intervalo correspondiente para un formato de 32 bits es 0,0000001192092896 ≈ 0,00000012.
0.0000000000000002 es mucho menor que 0.00000012. Por lo tanto, hay muchas más fracciones mixtas entre dos números enteros consecutivos (por ejemplo, 3 y 4) en el formato de 64 bits que entre dos números enteros consecutivos en el formato de 32 bits.
El número de fracciones mixtas entre dos números enteros consecutivos en la recta numérica es infinito. Por lo tanto, ningún formato (por ejemplo, 32 bits o 64 bits) puede proporcionar todas las fracciones mixtas entre dos números enteros consecutivos (números enteros). Cuanto menor sea el espacio (intervalo) entre dos números enteros consecutivos proporcionado por un formato (por ejemplo, 32 bits o 64 bits), mayor será el número de fracciones mixtas entre los números enteros consecutivos (para la recta numérica).
Las razones por las que el formato de 64 bits se describe como de doble o mayor precisión, en comparación con el formato de 32 bits, son que el intervalo entre dos fracciones mixtas consecutivas delimitadas por dos números enteros consecutivos para el formato de 64 bits es menor que los 32 correspondientes. Intervalo de formato de bits. Además, hay más fracciones mixtas posibles entre dos enteros acotados para el formato de 64 bits que para el formato de 32 bits.
Convertir una parte decimal (fracción) de un número decimal en una parte binaria
El 36.375 es un número decimal con la parte decimal “.375”. La parte decimal de “.375” es una fracción entre cero y uno. El 0,5 en base diez tiene el mismo valor que 1/2 en base dos. El 0,5 10 que se expresa con el desarrollo en base dos es:
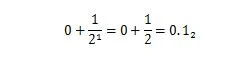
no es 0.101 2 lo que significa 0.625 10 . La parte decimal de un número decimal tiene su parte binaria equivalente para el número binario correspondiente. Entonces, para convertir un número decimal como 36,375 10 a base dos, convierta 36 a binario y luego convierta .375 también a binario. Luego, une ambos resultados con el punto binario. Los métodos para convertir las dos secciones son diferentes. En el capítulo 1 se explica cómo convertir un entero decimal a base 2.
Para convertir la fracción decimal a fracción binaria, siga los siguientes pasos:
- Multiplica la fracción decimal (parte decimal) por 2. El número entero que resulta de esto es el primer dígito binario.
- Repita el paso anterior con el resultado decimal fraccionario para obtener el siguiente dígito binario.
- Continúe repitiendo el paso anterior hasta que el resultado fraccionario decimal sea .0000—.
Ejemplo: convertir la parte fraccionaria de 36,375 10 a la parte fraccionaria equivalente en base dos.
Solución:
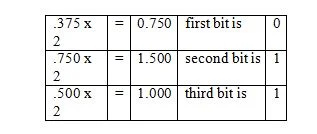
Tenga en cuenta que en el tercer paso se multiplicó .500 por 2 y no 1.500. La fracción binaria correspondiente se lee en la última columna desde arriba. Y entonces, el siguiente resultado es:
.375 10 = .011 2
Convertir una parte binaria (fracción) de un número binario en una parte decimal
Para lograr esto, expanda la fracción binaria en potencias recíprocas de 2.
Ejemplo: convertir la parte fraccionaria de 100100.011 2 a la parte fraccionaria equivalente en base diez.
Solución:
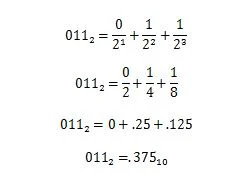
3.10 Prefijos numéricos en informática
En la vida normal, 1 kilo significa 1000, que se abrevia en k (minúscula) como en 1 kg. En informática, 1 kilo significa 2 10 = 1024, pero se abrevia en K (mayúscula) como en 1Kbits. En la vida normal, 1 mega significa 1.000.000 que se abrevia en M (mayúscula) como en 1Mg. En informática, 1 mega significa 2 20 = 1,048,576 = 2 10 x2 10 = 1024 x 1024 = 1.048.576 y todavía se abrevia en M (mayúscula) como en 1Mbits. En la vida normal, 1 giga significa 1.000.000.000 se abrevia en G (mayúscula) como en 1Gg. En informática, 1 giga significa 2 30 = 1,073,741,824 = 2 10 x2 10 x2 10 = 1024 x 1024 x 1024 = 1.073.741.824 y todavía se abrevia en G (mayúscula) como en 1Gbits. La siguiente tabla da el significado de cuatro prefijos en la vida normal y en la informática:
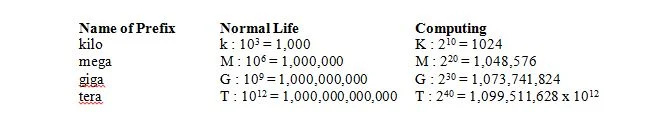
3.11 Problemas
Se recomienda al lector que resuelva todos los problemas de un capítulo antes de pasar al siguiente.
- Dibuja una recta numérica con números enteros de -10 a +10.
- Sume los siguientes números binarios en complemento a dos de 8 bits: 101010 2 y 1111 2 .
- Utilice únicamente el método del complemento a dos en 8 bits para restar el número binario de 1111 2 del número binario de 101010 2 .
- Encuentra el producto de 10110 2 x1101 2 en base dos.
- Dividir 36.375 10 por 1000 10 en decimal y en binario, y comparar los resultados.
- Utilice los 8 bits de su elección para ilustrar los lógicos AND, OR, XOR, Invertir, Desplazar a la derecha, Desplazar a la izquierda, Girar a la derecha y Girar a la izquierda. Cada byte debe tener una mezcla de unos y ceros.
- a) Escribe el código numérico del carácter ASCII de cero en hexadecimal, binario y decimal.
b) Escriba el código numérico para el carácter ASCII de “1” en hexadecimal, binario y decimal.
c) Escriba el código numérico del carácter ASCII de “A” en hexadecimal, binario y decimal.
d) Escriba el código numérico del carácter ASCII de “a” en hexadecimal, binario y decimal. - Convertir 49,49 10 en base dos. Convierta su resultado al formato de punto flotante IEEE de 32 bits.
- a) ¿En qué se diferencia el formato de punto flotante IEEE de 64 bits del formato de 32 bits?
b) Dé las dos razones relacionadas por las que el formato de 64 bits se describe como de doble o mayor precisión que el
Formato de 32 bits.